Октаэдр

Многогранник с восемью гранями.

Правильный октаэдр является одним из пяти выпуклых правильных многогранников, так называемых платоновых тел. Его грани — восемь равносторонних треугольников.

Дальше

Правильный октаэдр

факт

Двойственен кубу

факт

является полным усечением тетраэдра

факт

представляет собой квадратную бипирамиду в любом из трёх ортогональных направлений

факт

является треугольной антипризмой в любом из четырёх направлений

факт

редставляет собой трёхмерный шар в метрике городских кварталов

факт

трёхмерный вариант более общего понятия гипероктаэдр

О главном

Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.

Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

Октаэдр имеет следующие характеристики:

Отзывы

01 / 05

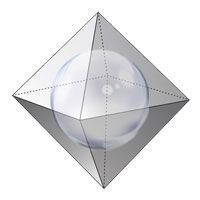
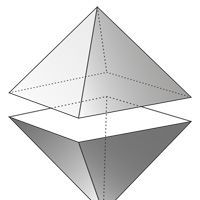
Октаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы октаэдра определяется по формуле:

Радиус описанной сферы октаэдра
R=a/2 √2, где a - длина стороны.
02 / 05

Сфера может быть вписана внутрь октаэдра.

Радиус вписанной сферы октаэдра определяется по формуле:

r=a/6 √6
03 / 05

Площадь поверхности октаэдра

Для наглядности, площадь поверхности октаэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон октаэдра (это площадь правильного треугольника) умноженной на 8.

Текст
04 / 05

Объем октаэдра определяется по следующей формуле:

V=a³/3 √2

Текст
05 / 05

Октаэдр можно представить в виде двух правильных пирамид с четырехугольным основанием, соединенных друг с другом через это основание.

Текст

Октаэдр

Правильный октаэдр

факт

факт

факт

факт

факт

факт

О главном

Октаэдр имеет следующие характеристики:

Отзывы

Октаэдр чаще встречается в природе: